Caudal, pressão e altura manométrica são conceitos hidráulicos fundamentais para analisar a performance de uma bomba.

Caudal
Caudal é a quantidade de líquido que passa através de uma bomba dentro de um determinado período de tempo. No desempenho de uma bomba, podemos distinguir entre dois parâmetros de caudal: Caudal volumétrico e caudal mássico.
Caudal Volumétrico (Q)
Caudal volumétrico é o que se pode ler a partir de uma curva hidráulica de uma bomba. Uma bomba consegue mover um volume por unidade de tempo (medido em m³/h), independentemente da densidade do líquido. Por exemplo quando lidamos com abastecimento de água, o caudal volumétrico é o parâmetro mais importante, porque precisamos que a bomba forneça um determinado volume de água para consumo humano ou rega.
\begin{equation} \label{eq:caudal} \Large
Q=\frac { { Q }_{ m } }{ \rho }
\end{equation}
Caudal Mássico (Qm)
O caudal mássico é a massa que uma bomba move por unidade de tempo, medida em kg/s. A temperatura do líquido tem influência sobre quão grande a massa do que pode fluir pela bomba opor unidade de tempo, pois a densidade de um líquido muda com a temperatura. De forma equivalente aos sistemas de aquecimento, refrigeração e ar condicionado, o caudal de massa é o portador de energia.
\begin{equation} \label{eq:caudal2} \Large
{ Q }_{ m }=\rho \cdot Q
\end{equation}
Pressão (p)
A pressão é uma medida de força por unidade de área. Distinguem-se pressão estática, pressão dinâmica e pressão total. A pressão total é a soma da pressão estática com a pressão dinâmica:
\begin{equation} \label{eq:ptot} \Large
{{p}_{tot}\mathrm{{=}}{p}_{est}\mathrm{{+}}{p}_{din}}
\end{equation}
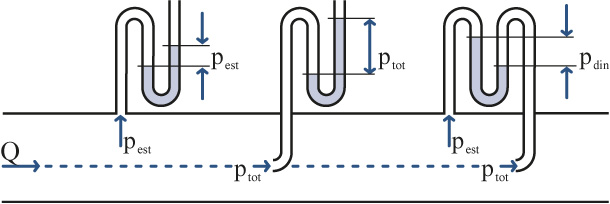
Figura 1 Pressão estática, pressão dinâmica e pressão total
Pressão Estática
A pressão estática é medida com um manómetro colocado perpendicular ao fluxo do líquido ou numa situação estática em que o líquido está sob pressão.
Pressão Dinâmica
A pressão dinâmica é causada pela velocidade do líquido, que não pode ser medida por um manómetro normal. É calculada pela seguinte fórmula:
\begin{equation} \label{eq:pdin} \Large
{ p }_{ din }=\frac { 1 }{ 2 } \cdot \rho \cdot { v }^{ 2 }
\end{equation}
Onde:
ρ é a densidade do líquido em [kg/m³]
v é a velocidade do líquido em [m/s]
A pressão dinâmica pode ser convertida em pressão estática, reduzindo a velocidade do líquido e vice-versa.
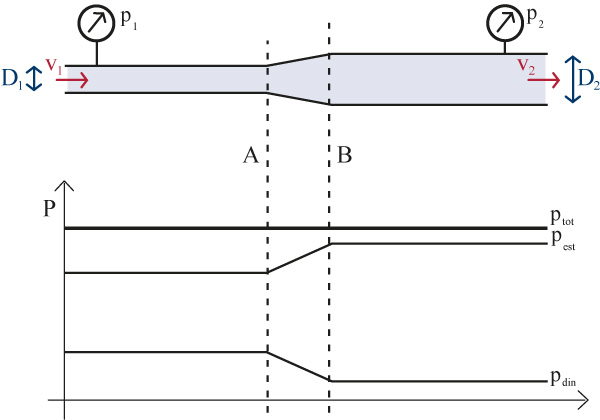
Figura 2 Pressão estática e pressão dinâmica em relação ao diâmetro do tubo
A figura 2 mostra uma parte de um sistema em que o diâmetro do tubo aumenta de D1 para D2, resultando numa diminuição na velocidade da água, de v1 para v2. Assumindo que não há perdas for atrito no sistema, a soma da pressão estática e da pressão dinâmica é constante ao longo do tubo.
\begin{equation} \label{eq:pconst} \Large
{ p }_{ 1 }+\frac { 1 }{ 2 } \cdot \rho \cdot { v_{ 1 } }^{ 2 }={ p }_{ 2 }+\frac { 1 }{ 2 } \cdot \rho \cdot { v_{ 2 } }^{ 2 }
\end{equation}
Então, um aumento no diâmetro do tubo, como a mostra a figura 2 resulta num aumento na pressão estática que é medido no manómetro p2.
Na maioria dos sistemas de bombagem, a pressão dinâmica tem um impacto pequeno sobre a pressão total. Por exemplo, se velocidade de um fluxo de água é de 4,5 m/s, a pressão dinâmica é cerca de 0,1 bar, o que é considerado insignificante em grande parte dos casos.
Medição de Pressão
A pressão é medida, por exemplo, em Pa (N/m²), bar (10^5 Pa) ou PSI (lb/pol²). Ao lidar com a pressão que é importante saber o ponto de referência para a medição de pressão. Dois tipos de pressão são essenciais em relação com a medição da pressão. Pressão absoluta e pressão relativa (ou efetiva).
Pressão Absoluta (Pabs)
A pressão absoluta é definida como a pressão acima do vácuo absoluto, 0 atm. Normalmente, o valor de "pressão absoluta" é utilizada nos cálculo de cavitação.
Pressão Relativa (ou Pressão Efetiva)
A pressão relativa é a pressão maior do que a pressão atmosférica (1 atm). Um manómetro convencional mede a pressão relativa, medindo a diferença de pressão entre o sistema e a atmosfera. Normalmente quando se fala de pressão, estamo-nos a referir à pressão relativa.
Pressão Diferencial
A pressão diferencial é a diferença de pressão entre as pressões aferidas em dois pontos, por exemplo, quedas de pressão provocada por um sistema de válvulas, nas mesmas unidades da pressão.
Altura Manométrica (H)
A altura manométrica de uma bomba representa qual a altura que uma bomba consegue levantar um líquido. A altura manométrica é medida em metros (m) e é independente da densidade do líquido. A seguinte fórmula mostra a relação da pressão (p) e a altura manométrica (H):
\begin{equation} \label{eq:hp} \Large
H=\frac { p }{ \rho \cdot g }
\end{equation}
em que:
H é a altura manométrica em [m]
p é a pressão em [Pa = N/m²]
ρ é a densidade do líquido em [kg/m³]
g é a aceleração da gravidade em [m/s²]
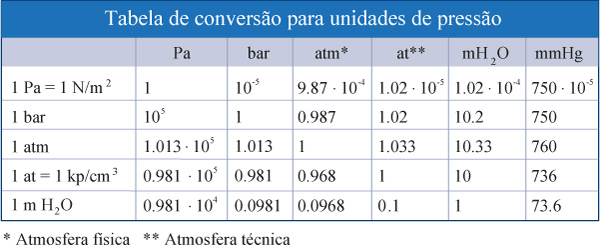
Normalmente, a pressão é medida em [bar], que é igual 10^5 Pa. No entanto, outras unidades de pressão são utilizadas como mostra a Tabela 1.
A relação entre a pressão e a altura manométrica é mostrado na figura 3 onde é bombeado quatro liquídos com densidades diferentes.
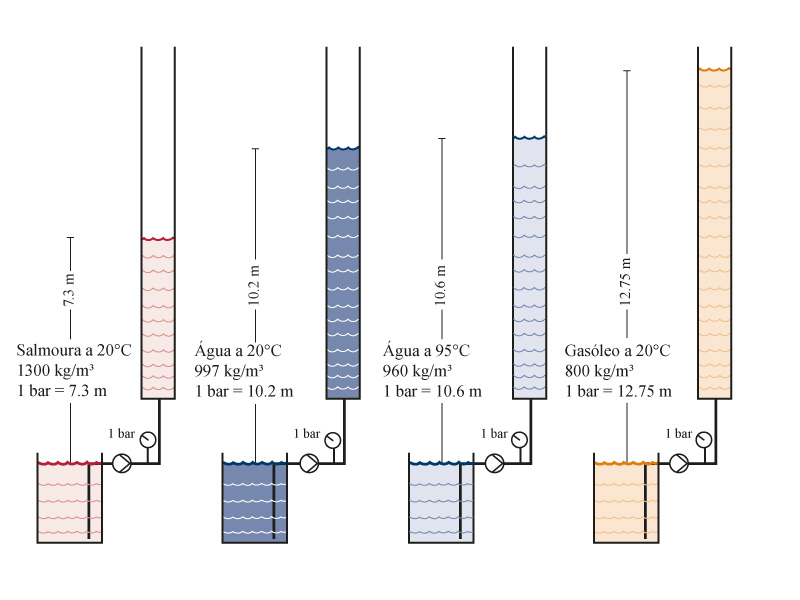
Figura 3 Bombear liquidos diferentes a 1bar correspondem diferentes alguras manométricas
Como Determinar a Altura Manométrica
A altura manométrica da bomba é determinado através da leitura da pressão na parte superior da bomba P2, na parte inferior P1 e de seguida converter os valores para altura manométrica - veja a figura 4. No entanto, se existe diferença geométrica na altura manométrica entre os dois pontos de medição, como é caso na figura 4, é necessário para compensar a diferença. Além disso, se as dimensões da abertura dos dois pontos de medição são diferentes também se tem de levar isso em conta.
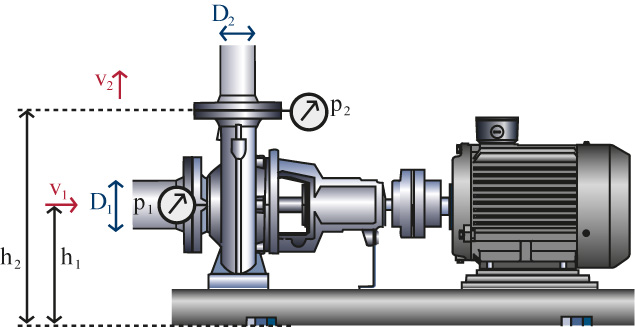
Figura 4 Bomba Centrifuga
A altura manométrica real da bomba (H) é calculada pela seguinte fórmula:
\begin{equation} \label{eq:alturamanometrica} \Large
H=\frac { { p }_{ 2 }-{ p }_{ 1 } }{ \rho \cdot g } +(h_{ 2 }-h_{ 1 })+\frac { { v_{ 2 } }^{ 2 }-{ v_{ 1 } }^{ 2 } }{ 2\cdot g }
\end{equation}
em que:
H é a altura manométrica real da bomba em [m]
p é a pressão em [Pa = N/m²]
ρ é a densidade do líquido em [kg/m³]
g é a aceleração da gravidade em [m/s²]
h é a altura geométrica, [m]
v é a velocidade do líquido em [m/s]
A velocidade v líquido é calculado pela seguinte fórmula:
\begin{equation} \label{eq:velocity} \Large
v=\frac { Q }{ A } =\frac { 4\cdot Q }{ \pi \cdot { D }^{ 2 } }
\end{equation}
em que:
v é a velocidade do líquido em [m/s]
Q é o caudal de volume em [m³/s]
D é o diâmetro da porta em [mm]
Combinando essas duas fórmulas, altura manométrica (H) depende dos seguintes fatores: As medições de pressão p1 e p2, a diferença de altura entre a medição geométrica (h2-h1), o caudal (Q) através da bomba de e o diâmetro das duas portas D1 e D2.
\begin{equation} \label{eq:combinedformulas} \Large
H=\frac { { p }_{ 1 }-{ p }_{ 2 } }{ \rho \cdot g } +(h_{ 2 }-h_{ 1 })+\frac { 8\cdot Q^{ 2 } }{ g\cdot \pi ^{ 2 } } \cdot \left( \frac { 1 }{ { D_{ 2 } }^{ 4 } } -\frac { 1 }{ { D_{ 1 } }^{ 4 } } \right)
\end{equation}
A correção devido à diferença de diâmetro porta é causada pela diferença na pressão dinâmica.
Exemplo de Cálculo
Uma bomba do mesmo tipo que o mostrado na figura 4 é instalado num sistema com os seguintes dados:
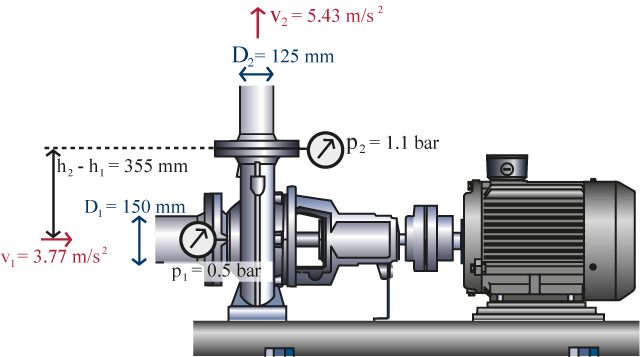
Figura 5 Cálculo da altura manométrica
Q = 240 m3/ h
p1 = 0,5 bar
p2 = 1,1 bar
Líquido: água a 200ºC
Sucção de diâmetro D1 = 150 mm
Descarga porta diâmetro D2=125 mm
A diferença de altura entre os dois portos onde os medidores de pressão são instalados é
h2 - h1= 355 mm
Estamos agora em condições de calcular a altura manométrica da bomba:
\begin{equation} \label{eq:calc}
H=\frac { 1,1{ 1\cdot { 10 }^{ 5 } }-0,5\cdot { 10 }^{ 5 } }{ 998\cdot 9,81 } +(0,355)+\frac { 8\cdot Q^{ 2 } }{ 9,81\cdot \pi ^{ 2 } } \cdot \left( \frac { 1 }{ 0,125^{ 4 } } -\frac { 1 }{ 0,150^{ 4 } } \right) \\ H=6,13+0,36+0,77=7,26 m
\end{equation}
A diferença de pressão medida pelos manómetros em altura manométrica é de cerca de 1,1m inferior (7.26-6.13) que ao bomba está efetivamente a produzir. A razão pelo desvio é que em primeiro lugar, existe uma diferença de altura entre os manómetros (0,36 m) e em segundo lugar, é causada pela diferença de dimensões das porta, que neste caso representa uma altura manométrica de 0,77 m .
Se os manómetros estão colocados na mesma altura geométrica, não é necessário para compensar a diferença de altura (h2-h1). Muitas vezes a entrada e a saída são tem a mesma altura bem como as duas portas muitas vezes tem o mesmo diâmetro. Para estes tipos de bombas é usada a fórmula simplificada para determinar a altura manométrica:
\begin{equation} \label{eq:alturamanometrica2} \Large
H=\frac { { p }_{ 2 }-{ p }_{ 1 } }{ \rho \cdot g }
\end{equation}
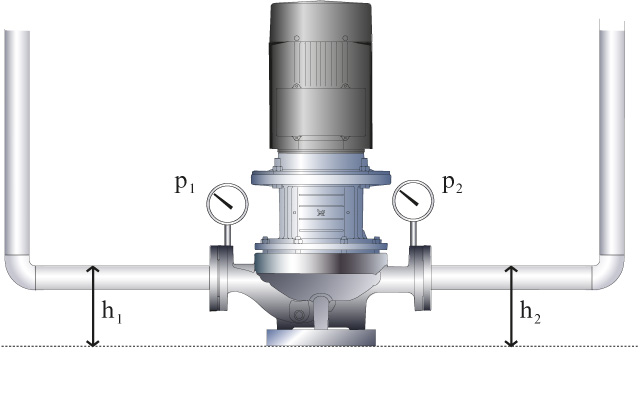
Figura 6 Bomba com a mesma altura geométrica na medição de pressão.